Matematikusok: Nem létezhet, hogy Biden michigani eredményei természetes eredetűek legyenek
2020.11.06. 12:00
Sírnak a statisztikusok Biden számait látva: a szavazatok eloszlása olyan szinten megy szembe mindennel, ami természetes, hogy ordít róla, hogy fentről nyúltak bele.
Benford törvényéről röviden azt lehet elmondani, hogy az arra épülő teszttel egyértelműen kimutatható egy számsorról, hogy ténylegesen véletlenszerű az eloszlása, vagy fentről belenyúltak – legyen az választási csalás vagy egy parkban előforduló virágok száma négyzetméterenként.
Biden számai nemhogy roppant gyanúsak, de szétszakítják az eloszlást:
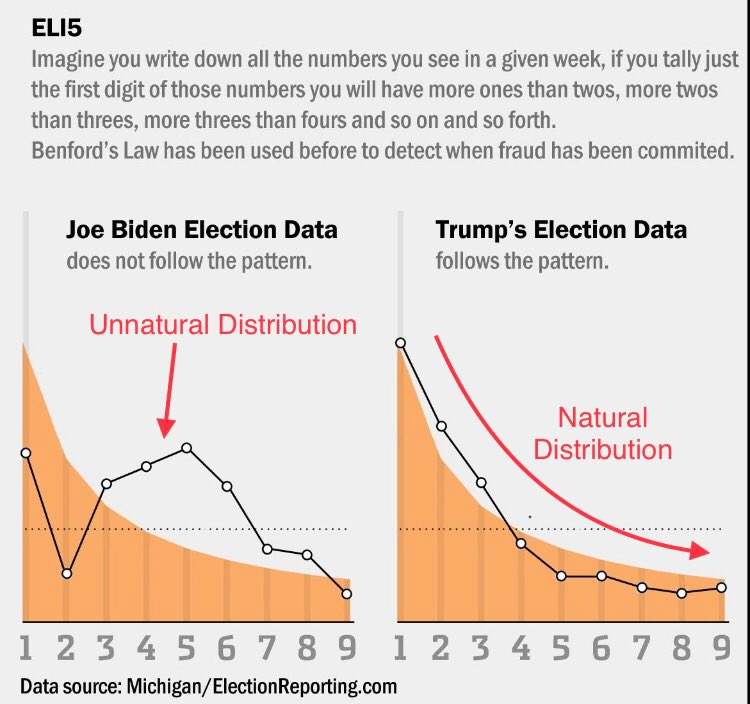
Ráadásul mindez véletlenül pont abban a tagállamban, Michiganben, ahonnan a legtöbb csalásgyanús visszajelzést kapta a kormány. Érdekes módon
De mi is Benford törvénye, más néven Newcomb–Benford-anomáliatörvény?
Kicsit bonyolult, de érdemes megérteni, mert ez az a teszt, amely a legbiztosabban kimutatja valamiről, hogy természetes eloszlásról van szó, vagy emberi kreációról. Nálam sokkal jobban elmondja a Numberphile YouTube-csatorna:
(Ugyanennek a csatornának van egy kilenc évvel ezelőtti videója is a Benford’s Law-ról, kifejezetten a választási csalásokra kihegyezve.)
Magyarul: ha az embereknek azt mondjuk, hogy írjanak le véletlenszerűen mondjuk ötven darab négyjegyű számot, és megnézzük azoknak az első számjegyét, akkor vajon melyik szám fog a leggyakrabban szerepelni az első helyen?
„Tulajdonképpen bármelyik szerepelhet”, gondolod, és teljesen igazad van: ugyanis az ember úgy gondolkodik, hogy biztos véletlenszerűnek tűnik, ha minden számot felhasznál véletlen előfordulási gyakorisággal.
De ez nem így van: a matematika egyik régóta ismert anomáliája, hogy minden természetes – tehát nem tudatos tervezésű – számsorozatban a legtöbb szám egyessel kezdődik, ezt követi a kettes, és így tovább.
Hogy ez mennyire általános, jól mutatja, hogy bármilyen, semmiféle algoritmikus szabályt nem követő adatsorra ráillik.
Bármilyen eredetű legyen is egy szám – például tavak felszíne, az egész számok négyzetgyökei –, körülbelül hatszor olyan gyakran kezdődik 1-gyel, mint 9-cel. A számok kb. 31%-a kezdődik 1-gyel, 19%-a 2-vel, 12%-a 3-mal, és a százalékok a számok nagyságával egyre csökkennek.
Ez nem azt jelenti, hogy az univerzumban van valami nem véletlenszerű, hanem azt, hogy az emberek által megalkotott tízes számrendszerben így realizálódik az a véletlenszerűség, ami a természetben tapasztalható.
Vagyis minden, ami tudatos emberi tervezés eredménye, nem Benford-eloszlású, például:
- a rendszámok,
- a telefonszámok,
- a bizonyítványok,
- a háziállatok száma családonként,
- Biden választási eredményei a billegő tagállamokban.
Benford-eloszlású viszont minden természetes, nem emberi tervezésű számsor:
- a világ országainak lakossága,
- a tőzsdei eladások,
- a Finnország tavainak partjain található mökkik száma,
- a világtörténelem összes demokratikus szavazása,
- Biden választási eredményei a nem billegő tagállamokban.